無料の電磁界解析ソフトfemmで基本的な電磁界解析を行いました。
磁気回路の理解や、シミュレーションを学習する際の参考となればと思います。
femmの概要
femmは無料の電磁界解析ソフトです。
電磁界解析は、磁束の動きを確認するために用いられます。
電流と比較して、磁束は磁路から漏れやすいです。また磁路の形成に用いられる鉄には、飽和という現象があります。飽和が起こると、磁束がほとんど流れなくなります。つまり電気回路で電流を考えるように、磁気回路で磁束を考えても中々上手くいかないことが多くあります。
このような場合でも電磁外解析であれば磁束の流れを確認することができます。
以下の研究室ページが他のソフトを確認する上でも参考となりました。
ダウンロード
以下のサイトから、64bit版をダウンロードしました。
手法・条件
”magnetics problem”で解きます。また条件は、磁束を手計算で計算できるものとします。
以下のYouTube動画と全く同様の手順で入力・計算を行います。
結果
シミュレーション結果は、以下の図のようになりました。おおよそ動画と同じ結果となっています。
図からも、鉄の部分の磁束密度が、2 T(テスラ)程度となっていることが分かります。この磁束密度では鉄は磁気飽和(鉄の透磁率が非常に小さくなる現象)しています。
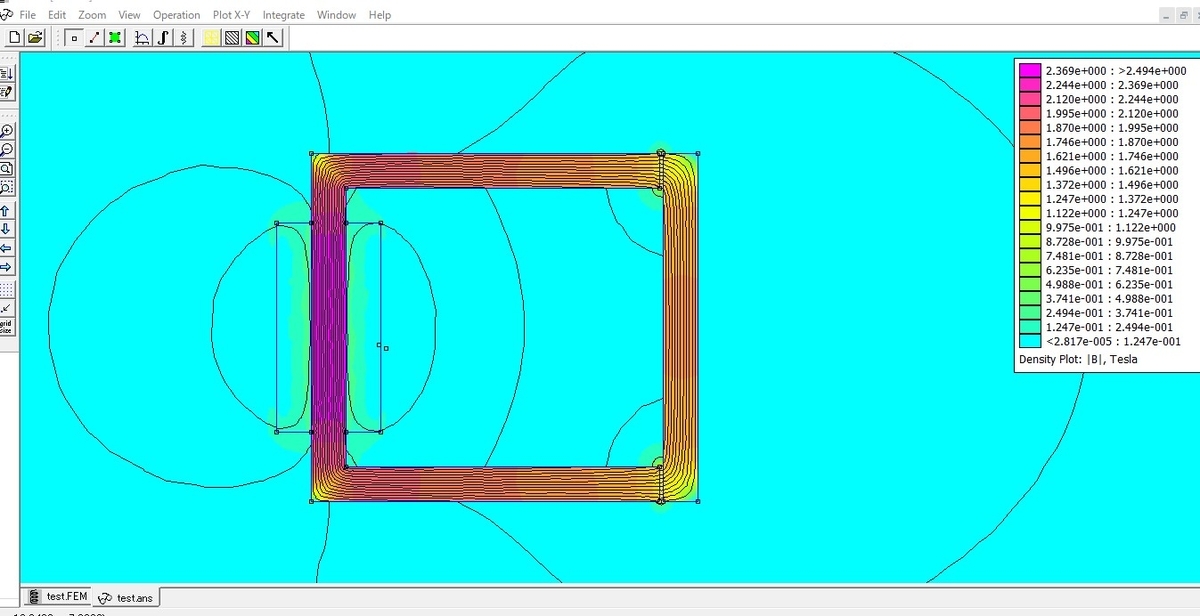
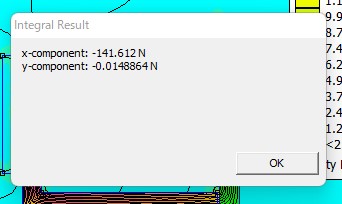
また、「左側のコの字形の鉄」が「右側の鉄の棒」を引く力は141 Nとなりました。これも上記の動画とほとんど同じ結果です。
磁気回路法による手計算
磁気回路法によってシミュレーションの結果を確認してみます。
動画の条件では、鉄が飽和してしまいます。鉄が飽和すると手計算が行えないので、鉄が磁気飽和しないようにします。逆に、鉄が磁気飽和し手計算が行えない場合に、シミュレーションを実施する有用性が高くなります。
具体的には、電流値のみを50Aから0.05Aへと変更してシミュレーションします。これによって、鉄の磁気飽和がなくなります。
電磁界解析結果(磁気飽和なし)
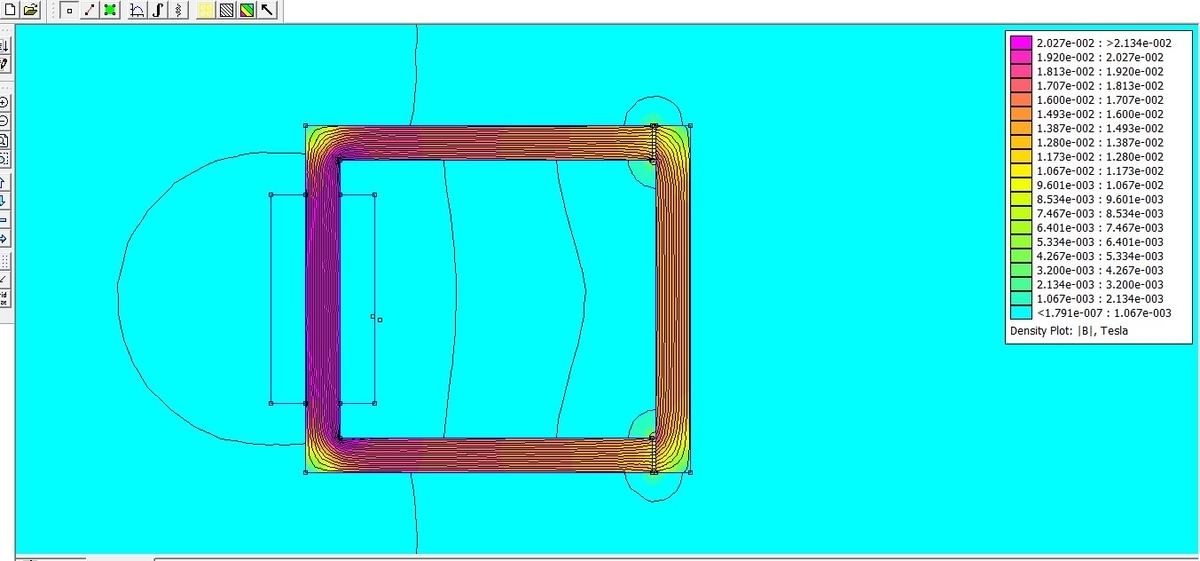
電流値のみを50Aから0.05Aへと変更したシミュレーションの結果を以下に示します。
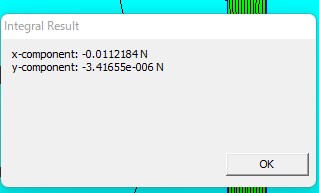
ギャップの部分(「コの字の鉄」と「鉄の棒」の間の隙間)の磁束密度は、おおよそ1.2×10-2 Tとなっています。また、「左側のコの字形の鉄」が「右側の鉄の棒」を引く力は、0.0112 Nとなります。
磁気回路法
磁気回路法で手計算をおこなった結果は、磁束密度が1.31×10-2 Tとなります。また、「左側のコの字形の鉄」が「右側の鉄の棒」を引く力は、0.0137 Nとなります。これは、かなりシミュレーションの結果と近い値となります。
なお鉄の磁気飽和やギャップの拡大(漏れ磁束の増大)などが重なると、磁気回路法による簡単な手計算での計算結果の精度がどんどん落ちていきます。
磁気飽和しない条件でのシミュレーションと手計算の比較結果は以下のとおりとなります。結果の値は近いものとなります。なお手計算の過程は雑ですがAppendixに記載しています。
| 手法 | ギャップ磁束密度(T) | 鉄の棒にかかる力(N) |
|---|---|---|
| 電磁界解析結果(シミュレーション) | 1.2×10-2 | 0.0112 |
| 磁気回路法(手計算) | 1.31×10-2 | 0.0137 |
まとめ
無料の電磁界解析ソフトのfemmを使用してみました。
先にも紹介しましたが、下記の動画が導入としては有用です。
このページを下記のAppendixも含めて参考にしていただけましたら幸いです。
Appendix
・日本語でfemmの使用法を紹介しているブログ
日本語で使用イメージが知りたい場合に参考となりました。
モデルは手計算しづらそうなので、上記の動画の条件の方がよいと思います。
・実際の使用例
高知工科大学の方の使用例です。
・femmのマニュアル
英語ですがfemmのマニュアルです。
磁気回路法による手計算に必要な学習
磁気回路法による力の手計算には「マクスウェル応力」と「磁気回路法」の知識が必要です。最後に示す計算も、以下の参考書の知識をベースに行うことが可能です。
これらの知識は、基本的な電磁気学がベースとなります。高校レベル(「物理のエッセンス」レベル)の電磁気学の知識があれば、手計算を行うために必要な「マクスウェル応力」や「磁気回路法」をイメージする上で問題はありません。
ただし、しっかりと時間をかけて基礎を身に着けたい場合は、以下に示す「電磁気学」などがオススメです。この過程は飛ばしても、「電磁気学演習」と「電動機・発電機の理論」の該当部分を眺めると磁気回路法の計算は行えるようになります。
基本が身についている場合は、「マクスウェルの応力」については以下に示す「電磁気学演習」の第三章が特に参考になります。
また、「磁気回路法」については以下に示す電気機器学の参考書(「電動機・発電機の理論」)が特に参考になります。
磁気回路法による手計算手法
かなり雑ですが、手計算の過程をいかに画像で示します。
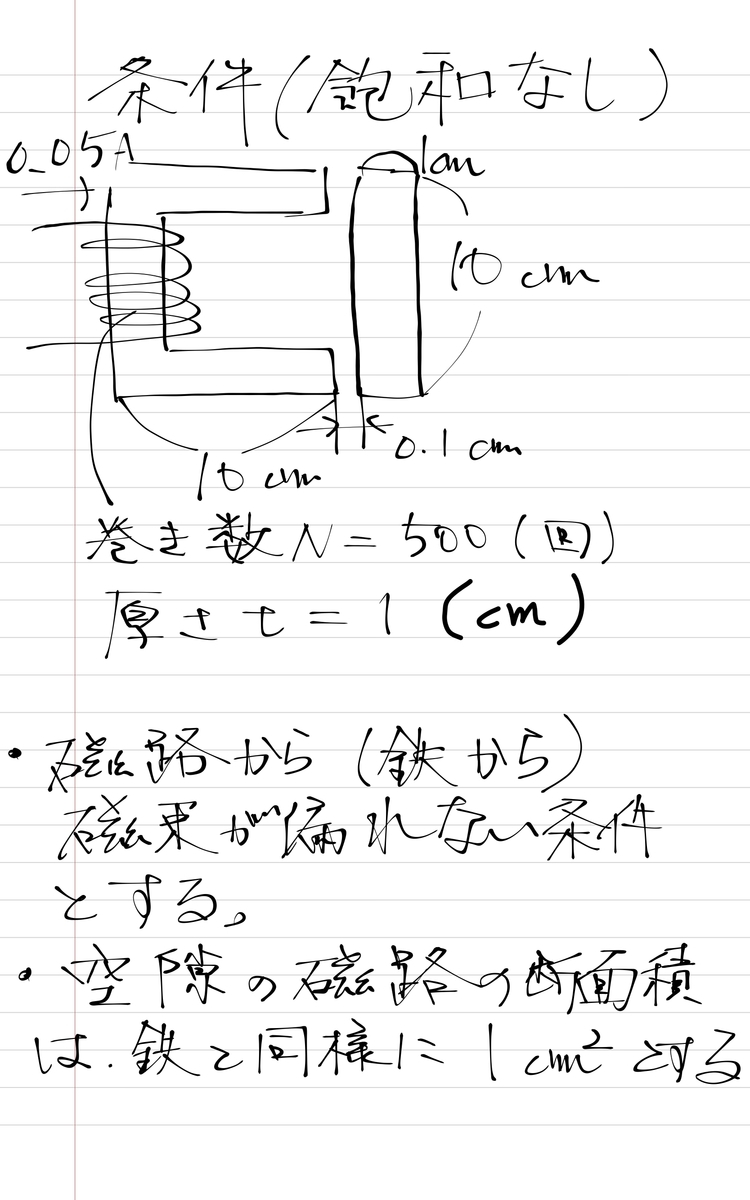
磁気回路法による手計算①:計算条件

(すみませんメンテ中です。)
磁気回路法による手計算②:右側の鉄の棒を引く力を求める。




・個人的なメモ事項
今後手書き入力を改善していくために記録。
タッチペン
タブレット
アプリ









